比特幣價格與時間存在關系？一文讀懂比特幣價值的對數增長模型_比特幣

原文：《偽造比特幣價值的對數增長模型》

摘要

本文探討了時間與比特幣價格之間是否存在關系。針對最小二乘假設，對提出的雙對數模型進行了統計有效性檢驗，使用Engle-Granger方法進行協整，以確保每個變量的平穩性以及潛在的虛假關系。除了這些測試中的一種以外，所有測試都可以反駁時間是比特幣價格一種重要預測因素的假設。

引言

各種來源提出了對數價格?對數時間模型來解釋比特幣價格走勢的很大一部分，因此提出了一種估計未來比特幣價格的機制。

科學方法對大多數人都是很難理解。這是違反直覺的。它可能會得出不反映個人信念的結論。理解這個基本的基本概念是該方法的基礎：錯誤是可以接受的。

根據偉大的現代科學哲學家卡爾·波普爾的觀點，為一種錯誤的結果檢驗一種假設是增加論點正確性的唯一可靠方法。如果嚴格和重復的測試不能表明假設是不正確的，則對于每個測試，假設都具有較高的正確性。這個概念稱為可證偽性。本文旨在偽造比特幣價值的對數增長模型，該模型在中進行了基本定義。

注：

所有分析均使用Stata14執行。本文不充當財務建議。

定義問題

為了偽造一個假設，首先我們必須說明它是什么：

空假設：比特幣的價格是比特幣已存在天數的函數

替代假設：比特幣的價格不是比特幣存在天數的函數

的作者選擇通過在比特幣價格的自然對數和比特幣存在天數的自然對數上擬合普通最小二乘回歸來測試H0。兩個變量都沒有伴隨的診斷程序，也沒有任何確定的對數轉換推理。該模型沒有考慮由于非平穩性造成的虛假關系的可能性，也沒有考慮任何相互作用或其他混雜因素的可能性。

方法

芝商所（CME）將推出微型比特幣和以太坊期權:3月1日消息，芝商所（CME）宣布，計劃于3月28日推出微型比特幣和以太坊期權，目前正等待監管機構的審查。 （金十）[2022/3/1 13:30:53]

在本文中，我們將探索該模型并通過常規回歸診斷對其進行運行，并確定對數轉換是否必要或適當，并探討可能的混淆變量，交互作用以及對混淆的敏感性。

另一個將要探討的問題是非平穩性。平穩性是大多數統計模型的假設。這個概念即隨著時間的流逝，任何時刻都沒有趨勢，例如，相對于時間的均值沒有趨勢。

在平穩性分析之后，我們將探討協整的可能性。

符號

介質在數學符號方面相對有限。估計統計參數的常用符號是在上面放一個范圍。相反，我們將術語的估計定義為。例如β的估計值=。如果我們表示一個2x2矩陣，我們將像等進行操作。下標術語被@取代-例如，對于向量X中的第10個位置，我們通常將X下標10。我們寫成X@10。

普通最小二乘

普通最小二乘回歸是一種估計兩個或多個變量之間線性關系的方法。

首先，讓我們將線性模型定義為X的某個函數，該函數等于Y且存在一些誤差。

Y=βX+ε

其中Y是因變量，X是自變量，ε是誤差項，β是X的乘數。OLS的目標是估計β，以使ε最小。

為了使成為可靠的估計，必須滿足一些基本假設：

因變量和自變量之間存在線性關系

這些錯誤是同調的

誤差的平均分布為零

錯誤中沒有自相關

線性度

我們首先看一下價格v天的非變換散點圖。

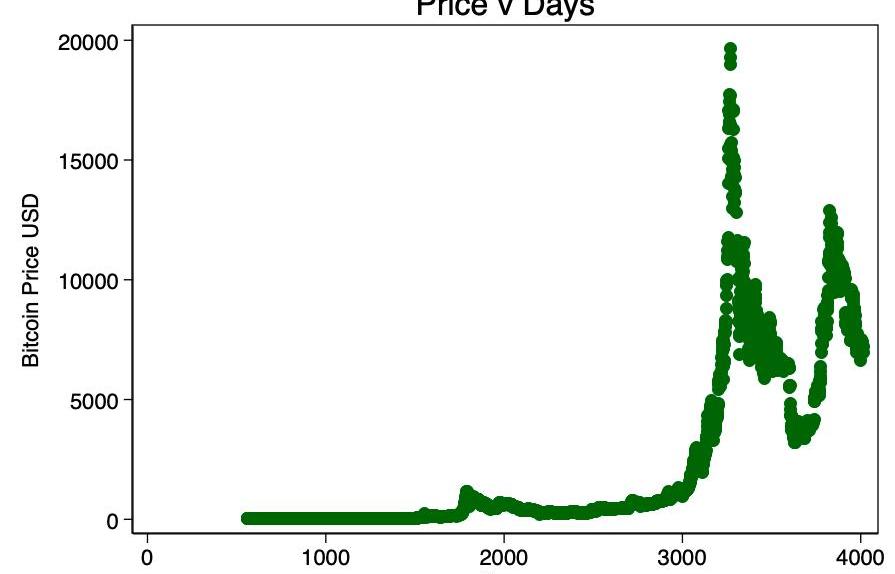
圖1-價格v天。數據分布范圍太廣，無法通過視覺確定線性度。

Pepperstone主管：埃隆·馬斯克的回應對比特幣而言是一記打擊:墨爾本經紀公司Pepperstone研究主管Chris Weston ：特斯拉CEO埃隆·馬斯克的回應對比特幣而言是一記打擊，但也承認了加密貨幣的碳排放問題。(金十)[2021/5/13 21:56:21]

在圖1中，我們遇到一個很好的理由來獲取價格的對數——跨度太寬了。取價格的對數并重新繪圖，使我們形成了熟悉的對數顯示模式

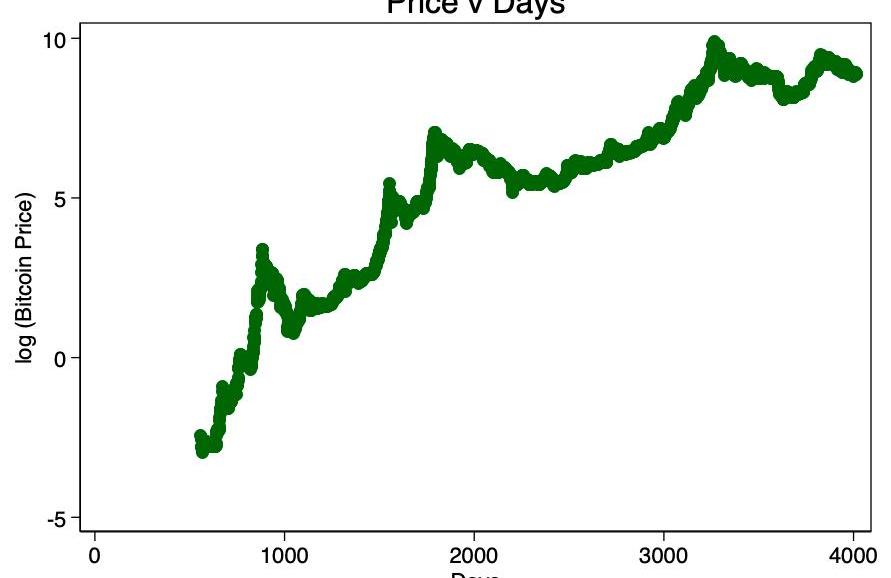
圖2-日志價格v天。一個清晰的對數模式正在出現。

取幾天的對數并再次作圖，得出了由圖3中的作者確定的明顯線性模式。

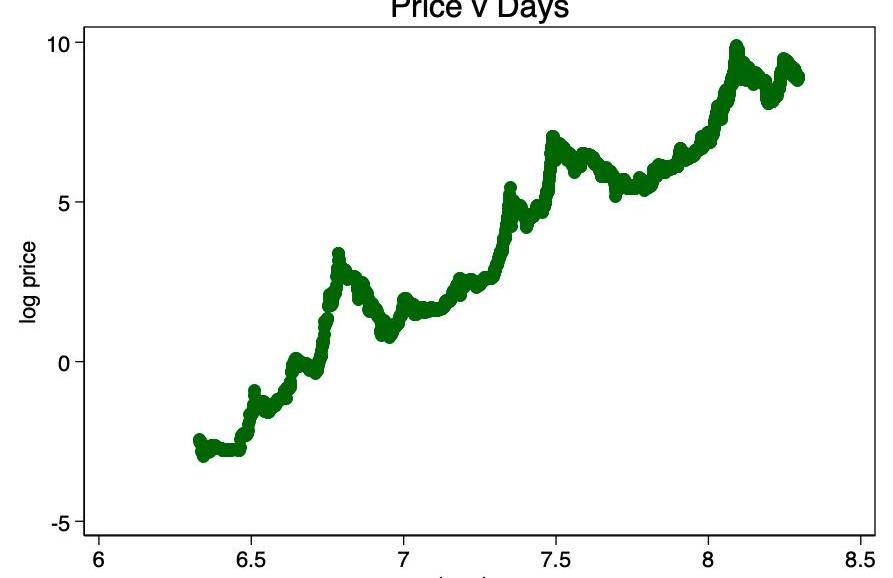
圖3—明顯的線性關系出現了

這證實了對數-對數的選擇——唯一真正顯示出良好線性關系的轉換。

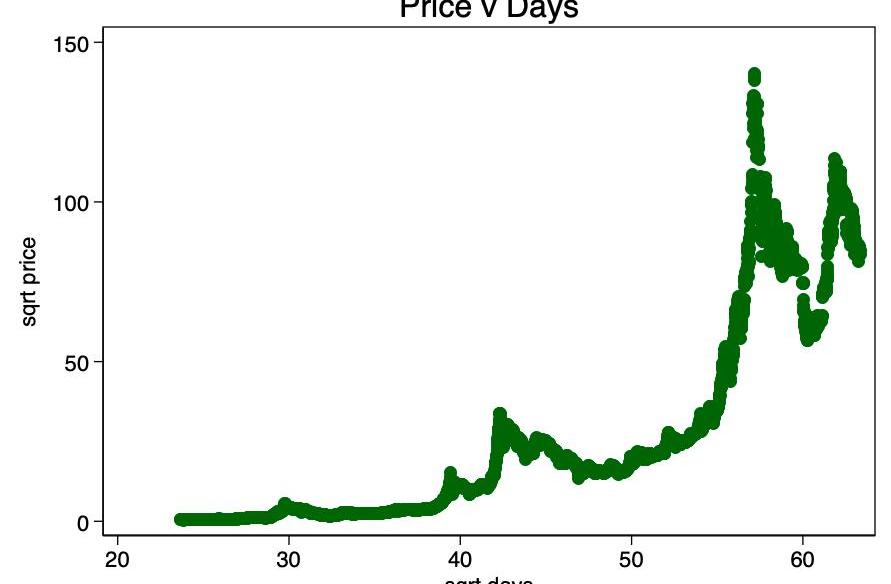
圖4–平方根變換比未變換的序列好很多

因此，初步分析不能否定H0。

對數-對數擬合回歸在下面的圖5中給出，其中=5.8

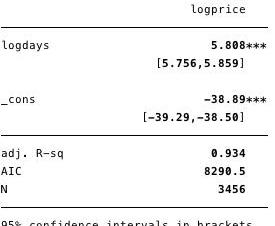
圖5—對數-對數回歸結果

使用該模型，我們現在可以估計殘差和擬合值并測試其他假設。

同質性

如果誤差項中恒定方差的假設為真，則對于預測值中的每個值，誤差項將在0附近隨機變化。因此，RVF圖是研究此假設準確性的簡單而有效的圖形方法。在圖6中，我們看到有一個巨大的模式，而不是隨機的散射，表明誤差項的非恒定方差。

聲音 | 加密技術分析師：自12月低點以來，萊特幣漲幅大于比特幣:加密技術分析師Marius Landman今日發推稱，自2019年12月17日的近期低點以來，比特幣上漲了28%，而萊特幣上漲了30%。萊特幣才是領先者，比特幣更強大只是人們的錯覺。[2020/1/8]

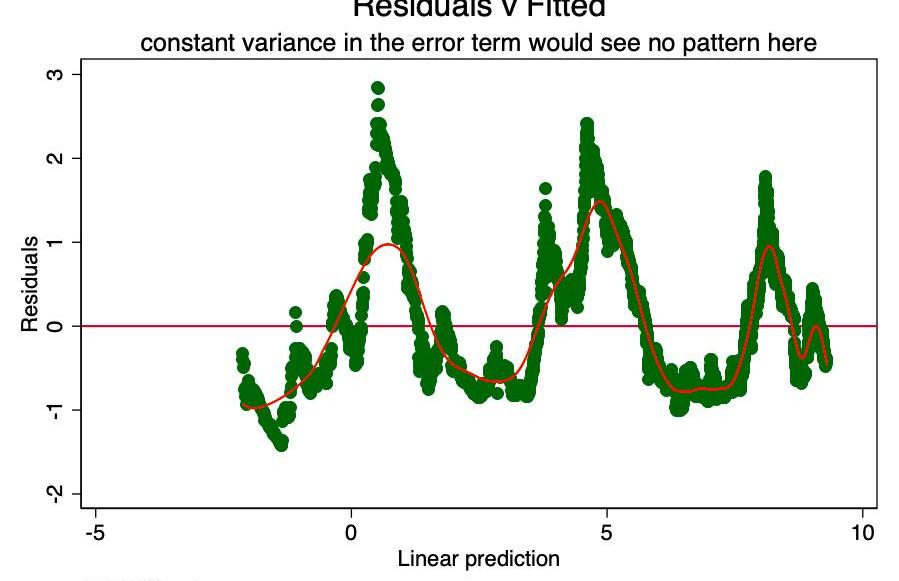
圖6a-RVF圖。此處的模式表示存在問題。

像這樣的異方差性會導致系數的估計值具有較大的方差，因此精度較低，并導致p值比應有的值大得多，這是因為OLS程序無法檢測到增大的方差。因此，當我們然后計算t值和F值時，我們使用了方差的低估值，從而導致較高的顯著性。這也會對的95％置信區間產生影響，該區間本身是方差的函數。

自相關的Breusch-Godfrey統計量也很重要，進一步為該問題提供了證據。

圖6b-檢測到的殘差中的自相關

在這個階段，通常是我們停止并重新指定模型的時候。但是，鑒于我們知道這些問題的影響，因此繼續進行回歸分析以了解存在這些問題將相對安全。我們可以通過多種方式來處理這些問題中的，例如自舉或使用健壯的估計器作為方差。

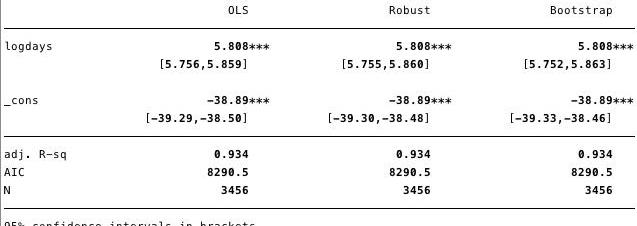
圖7—不同估計顯示了異方差的影響

如圖7所示，盡管方差有小幅增加，但在大多數情況下，存在的異方差實際上并沒有太大的有害影響。

誤差中的正常性

誤差項服從零均值正態分布的假設比線性或同方差不那么重要。非正態但不偏斜的殘差將使置信區間過于樂觀。如果殘差偏斜，那么您可能最終會有一點偏差。從圖8和9中可以看到，殘差嚴重傾斜。Shapiro-Wilk正態性檢驗的p值為0。它們不完全符合正態曲線，因此置信區間不受影響。

動態 | 比特幣全網未確認交易2906筆:據btc.com數據顯示，目前比特幣全網未確認交易數量為2906筆，比特幣全網算力為47.85EH/s，24小時交易速率為2.88txs/s。截至目前比特幣全球均價為4050.73美元，最近24小時漲幅為0.33%。[2019/3/23]

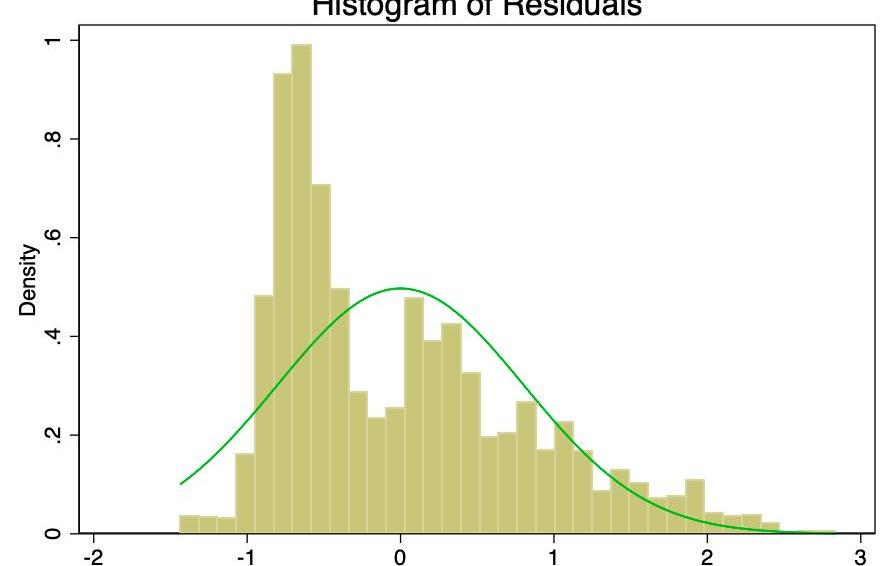
圖8-誤差項的直方圖，正態分布覆蓋。這個誤差項應該是正常的，但事實并非如此。

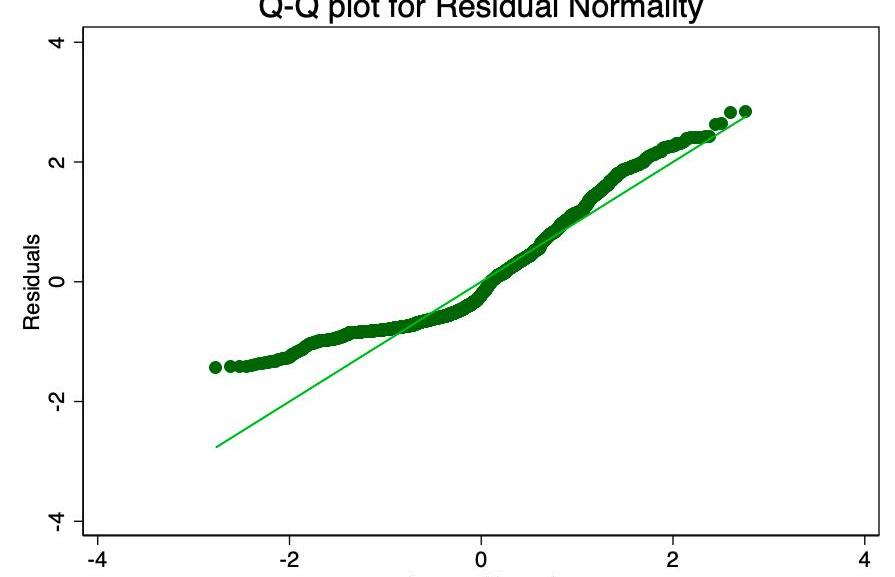
圖9-誤差項的正常分位數圖。點越接近直線，法線擬合越好。

杠桿作用

杠桿的概念是，并非回歸中的所有數據點都對系數的估計有同等的貢獻。某些具有高杠桿作用的點可能會根據是否存在來顯著改變系數。在圖10中，我們可以很清楚地看到，涉及點數太多。

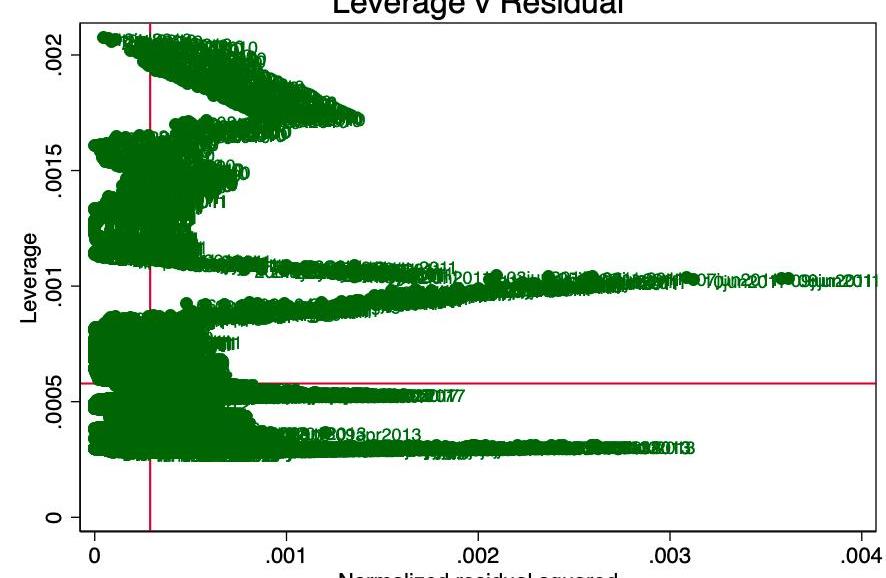
圖10-利用v平方殘差。

最小二乘摘要

基本診斷表明除了線性以外，基本上違反了所有高斯-馬爾可夫假設。這是拒絕H0的相對有力的證據。

穩定狀態

平穩過程被稱為集成了0級）。非平穩過程為I或更大。在這種情況下，集成更像是窮人的集成——它是滯后差異的總和。I表示，如果我們從序列中的每個值中減去第一個滯后，我們將有一個I過程。相對眾所周知，對非平穩時間序列的回歸可以導致虛假關系的識別。

在下面的圖12和圖13中，我們可以看到我們不能拒絕增強迪基·富勒檢驗的零假設。ADF檢驗的零假設是數據不穩定。這意味著我們不能說數據是固定的。

比特幣跌下9200美元:Bitfinex平臺目前比特幣價格為9183.6美元，漲幅3.5%。幣安平臺目前比特幣價格為9195美元，漲幅達3.72%。Bitstamp平臺比特幣價格為9183.49美元，跌幅為0.98%。[2018/4/28]

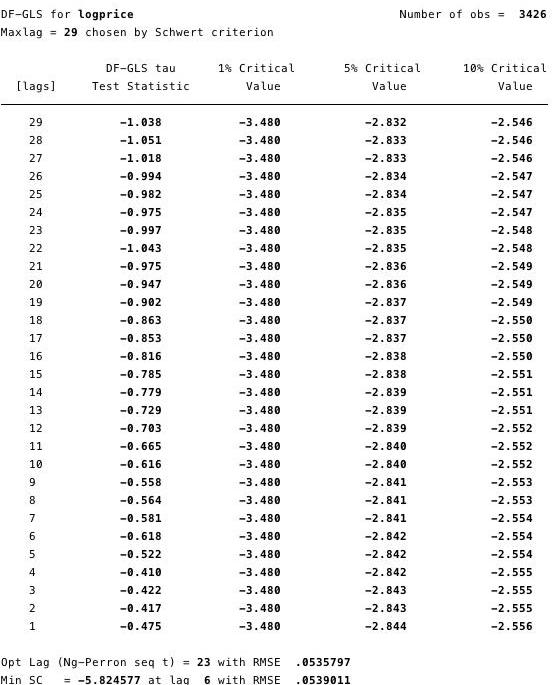
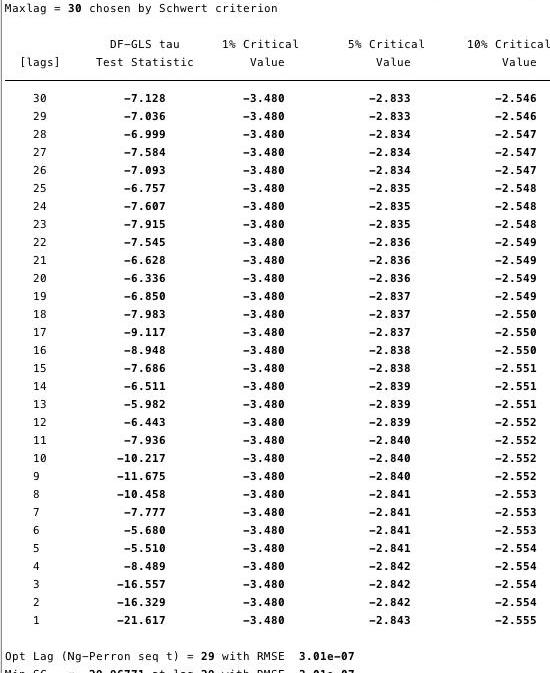
圖11和12–GLS增強了ADF測試，以記錄價格和記錄天數為單位根。

Kwiatkowski-Phillips-Schmidt-Shin測試是對ADF測試的平穩性的補充測試。該測試具有零假設，即數據是固定的。如圖13和14所示，我們可以拒絕兩個變量中大多數滯后的平穩性。

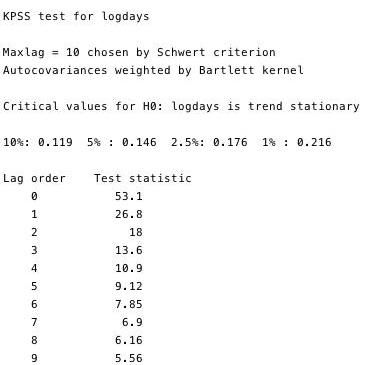
圖13和圖14—針對平穩性無效的KPSS測試

這些測試證明這兩個系列無疑是平穩的。這有點問題。如果該序列至少不是趨勢平穩的，那么OLS可能會誤導您識別虛假關系。我們可以做的一件事是獲取每個變量的對數日差并重建我們的OLS。然而，由于此問題在計量經濟學系列中相當普遍，因此我們可以使用更強大的框架——稱為協整。

協整

協整是一種處理一對I進程并確定是否存在關系以及該關系是什么的方法。為了理解協整，我們舉了一個醉漢和她的狗的簡化例子。想象一下，一個醉漢用皮帶牽她的狗回家。醉漢在各處走來走去，這只狗也隨機行走：嗅樹，吠叫，追逐抓撓。但是，狗的總體行進方向將在醉酒者的牽引帶范圍內。我們可以估計，在醉漢步行回家的任何地方，狗都會在醉漢的皮帶長度之內。這種糟糕的簡化是對協整的一個粗略比喻——狗和主人一起移動。

將其與相關性進行對比——假設流浪狗沿著醉酒走了95％的回家路程，然后跑去追著汽車駛向城鎮的另一側。流浪者與行走行徑之間將有很強的相關性，但是就像醉漢擁有許多晚上的床頭柜——這種關系并不意味著任何東西——它不能用來預測醉酒的出行地點，而在旅途的某些部分中，這是事實，而在某些部分中，這是完全不正確的。

為了找到醉漢，首先，我們將看到我們的模型應使用什么滯后規范。

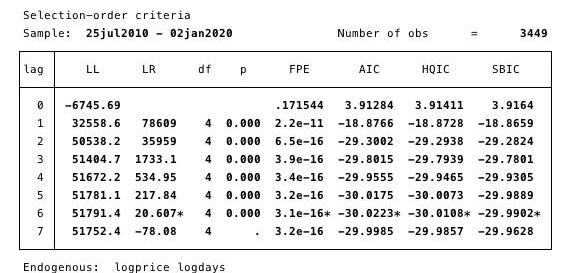
圖15-延遲階數說明。最小AIC用于確定。

我們在這里確定通過選擇最小AIC進行調查的最合適的滯后階數為6。

接下來，我們需要確定是否存在協整關系。簡單的Engle-Granger框架使此操作相對容易。如果測試統計量比臨界值更負，則存在協整關系。

圖16—測試統計量遠沒有小于任何臨界值

圖16中的結果沒有證據表明對數價格與對數天之間存在協整方程。

局限性

在這項研究中，我們沒有考慮任何混雜變量。鑒于以上證據，任何混雜因素都不太可能對我們的結論產生重大影響-我們可以拒絕H0。我們可以說“日志天數和日志比特幣價格之間沒有關系”。如果真是這樣，那么就會有一個共同的關系。

結論

鑒于違反了所有高斯馬爾科夫假設的有效線性回歸假設，并且沒有可檢測到的協整性，并且兩個變量都是非平穩的，因此有足夠的證據拒絕H0，因此沒有有效的線性回歸。對數價格和對數天數之間的線性關系，因此不能用來可靠地預測樣本估計價格。

引用文獻:

https://medium.com/coinmonks/bitcoins-natural-long-term-power-law-corridor-of-growth-649d0e9b3c94

https://medium.com/@intheloop/when-moon-rational-growth-ranges-for-bitcoin-ffaa94c9d484

https://twitter.com/davthewave/status/1125689778102386690?s=20

https://www.youtube.com/watch?v=NjTpHS5xLP8

Davidson,R.,andJ.G.MacKinnon.1993.EstimationandInferenceinEconometrics.NewYork:OxfordUniversityPress.

Durbin,J.,andG.S.Watson.1950.Testingforserialcorrelationinleastsquaresregression.I.Biometrika37:409–428.

Engle,R.F.andGranger,C.W.J.1987.Co-integrationandErrorCorrection:Representation,EstimationandTesting.Econometrica,Vol.55,pp.251–276.

MacKinnon,JamesG.1990,2010.CriticalValuesforCointegrationTests.Queen’sEconomicsDepartmentWorkingPaperNo.1227,Queen’sUniversity,Kingston,Ontario,Canada.Availableathttp://ideas.repec.org/p/qed/wpaper/1227.html.

Schaffer,M.E.2010.egranger:Engle-Granger(EG)andAugmentedEngle-Granger(AEG)cointegrationtestsand2-stepECMestimation.http://ideas.repec.org/c/boc/bocode/s457210.html

https://medium.com/burgercrypto-com/debunking-bitcoins-natural-long-term-power-law-corridor-of-growth-c1f336e558f6

Tags：比特幣IONAND比特幣價格比特幣是什么時候誕生的NATION價格Nomadland比特幣價格實時行情分析師

POL幣最新價格