學習筆記 | 零知識證明算法之PLONK——電路_PLO

最近研究了下零知識證明算法-PLONK。肚子里的墨水又增加了，記一下學習成果與新的體會，和大家共同學習---江小白。

現狀

近些年，各種新的零知識證明算法層出不出，各有各的特點，各有各的優勢。借用V神系列文章里的一張圖來簡單呈現下當前的零知識證明算法現狀。

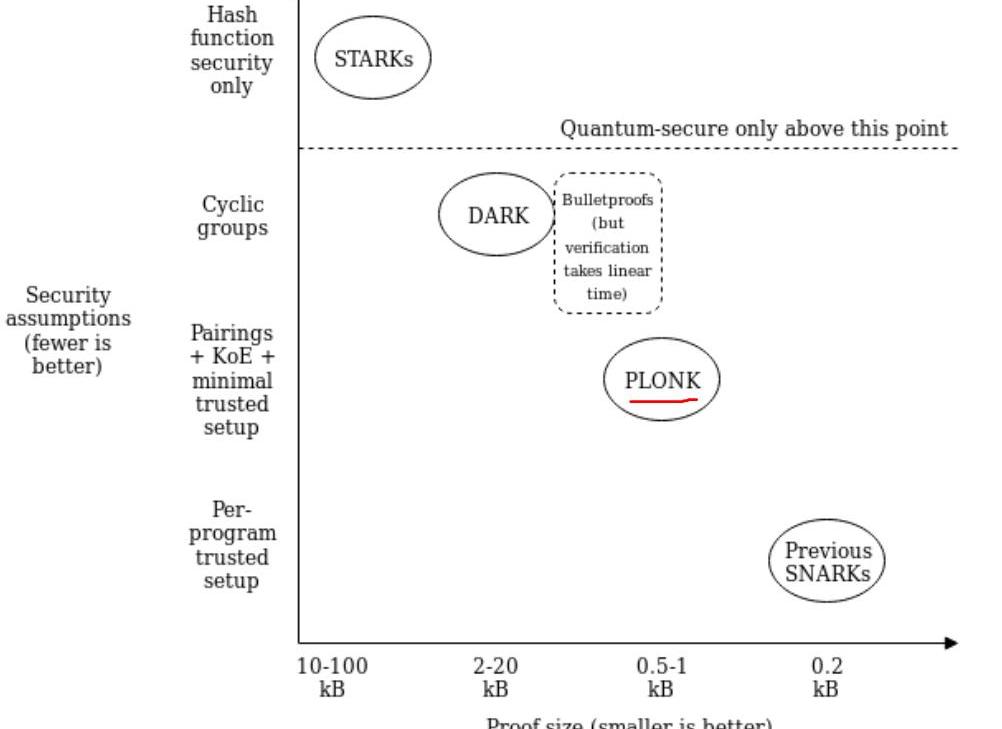
從圖中可以簡單總結出以下幾點：

理論上安全性最高的是STARKs算法，不依賴數學難題假設，具有抗量子性；Proof大小上最小的是SNARKs算法，如Groth16;PLONK算法在安全性上和Proof大小上，位于上述兩者之間；其他的這里不做過多闡述，如想了解零知識證明更多信息，可參考鏈接；對于SNARKs算法，繞不開的一個點就是中心化的TrustSetup，也稱之為CRS(theCommonReferenceString)。而無論是PGHR13,Groth16,還是GM17算法，它們的CRS都是一次性的，不可更新的。即，不同的問題將對應著不同的CRS，這在某些場景下，會變得比較麻煩。這些存在的問題，變成了PLONK，SONIC這類算法的一個優勢，它們算法雖然也需要中心化的可信設置，但是它的CRS具有一定的普適性。即，只要電路的大小不超過CRS的上限閾值，一些證明問題就可以共用一個CRS，這種CRS稱之為SRS(universalStructuredReferenceString)，關于SRS的定義，詳細的可參考SONIC協議里的第3小節。PLONK算法繼用了SONIC算法的SRS的思想，但是在證明的效率上，做了很大的提升。接下來，讓我們詳細的介紹下PLONK算法的具體細節，主要從下面四個小節去分享：

北京市委理論學習中心組：進一步擴大數字人民幣應用范圍:1月9日消息，北京市委理論學習中心組學習（擴大）會議舉辦構建新發展格局講座會議強調，用好產學研用資源，整合各方力量開展聯合攻關，力爭在大數據、區塊鏈、人工智能等關鍵底層技術領域取得新突破。國家金融科技基礎設施十分重要，要做好服務。用好大數據交易所，夯實底層數據基礎。應用場景是最好的催化劑，要深化發布和對接機制，支持金融科技在普惠金融、綠色金融、跨境貿易等領域推廣應用。進一步擴大數字人民幣應用范圍。(金十)[2023/1/9 11:02:11]

電路的設計--描述PLONK算法的電路的描述思想；置換論證或者置換校驗--復制約束，證明電路中門之間的一致性；多項式承諾--高效的證明多項式等式的成立；PLONK協議--PLONK協議剖析；電路

PLONK算法電路的描述和SONIC算法一直，具體的過程可以參考李星大牛的分享，已經寫的比較詳細且易懂。在這個小篇幅里，我想主要分享下我自己的兩點想法：

聲音 | Block.one首席人力資源官：快速學習是成功的關鍵因素之一:Block.one 今日在推特發布采訪James的視頻，并提到 “快速學習”是James成功的一個關鍵因素。James是Block.one的首席人力資源官。（MEET.ONE）[2019/12/12]

無論是什么樣的電路描述方式，電路的滿足性問題都要歸結于2點，門的約束關系和門之間的約束關系成立；在SNARKs系列的算法里，電路的描述單元都是以電路中有效的線為基本單元，具體的原理可以參考我之前分享的文章，而在PLONK，SONIC以及HALO算法里，電路的描述單元都是以門為基本單元。這兩種電路的不同描述方式帶來了一定的思考。那就是，之前在研究SNARKs算法時，我們都已經相信一個事實，“多項式等式成立，就代表著每個門的約束成立”，然后推斷，整個電路邏輯都是成立；在這個過程中，并沒有額外的去證明門之間的一致性成立；但是在PLONK算法里，除了要證明多項式等式成立外，還要額外的用置換論證的數學方法去證明門之間的約束關系，即復制約束。為何會有這樣的區別？希望有心的讀者能一起在評論區探討這個問題？我個人理解是因為電路的描述方式的不同：

動態 | 濟南市歷下區領導干部大會：加強區塊鏈等新知識學習:2月12日下午，濟南市歷下區召開全區領導干部大會。2019年，歷下區將在學習和實踐中不斷汲取能量、提高本領。通過加強產業金融、人工智能、區塊鏈等新理論、新知識的學習，著力增強專業思維、專業素養，努力做所在領域的專家、行家、實干家，在實踐中增才干。[2019/2/14]

PLONK算法里，電路描述的單元是門，它為每個門定義了自己的L,R,O，因此需要證明門之間的一致性；SNARKs算法里，電路描述的單元是線，門與門之間的值用的是同一個witness，因此不用額外證明一致性；置換論證

前面我們說過，在PLONK算法里，需要去證明門之間的約束關系成立。在做具體的原理解釋之前，我們先簡單的過一下PLONK協議的過程，如下圖所示：

可描述為：

根據電路生成三個多項式，分別代表這電路的左輸入，右輸入，輸出；利用置換校驗協議，去證明復制約束關系成立；步驟3和4，校驗門的約束關系成立。其中第1點已經在電路小節里闡述過了，接下來，將詳細的講解多項式置換校驗的原理。先從簡單的場景去講解：

動態 | 未來大學智慧學習工場旨在推動區塊鏈等新技術支撐下的產教融合創新:據中國經濟網報道，由教育部學校規劃建設發展中心和國研智庫共同發起，國家新一代人工智能戰略發展研究院、國家超級計算天津中心、天津大學、南開大學、聯合國和平大學等相關機構合作設立的產學研協同創新平臺——未來大學智慧學習工場，旨在推動區塊鏈等新技術支撐下的產教融合創新，探索我國應用型人才培養模式和現代職業教育體系。[2018/12/26]

單個多項式的置換校驗

其實就是證明對于某個多項式f，存在不同的兩個點x,y，滿足f(x)=f(y)。下面來看具體的原理：

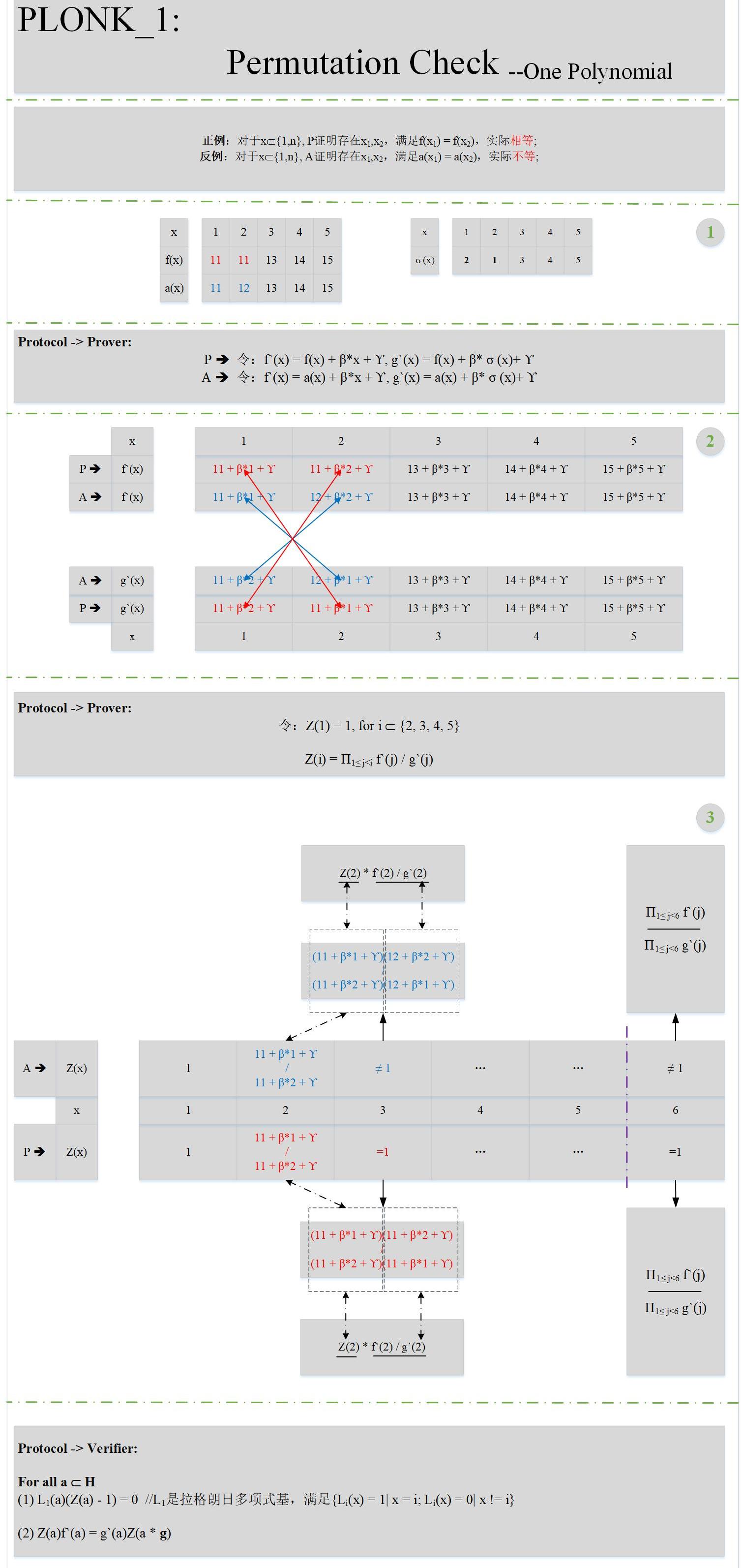
上圖中加入了一個正例P，一個反例A，方便大家理解置換校驗的原理。有幾點需要解釋的是：

而經過仔細剖析Z的形式，不難發現，Z(n+1)其實就是兩個函數所有值的乘積的比值(不知是否等同于V神文章里的坐標累加器？)。理論上是等于1。因此，我們需要設計這樣的一個多項式Z，需滿足：deg(Z)<n

傳真格基金創始人徐小平呼吁各CEO了解區塊鏈 學習如何擁抱這場革命:據某互聯網知名博主爆料，真格基金創始人徐小平在真格基金投資組合微信群呼吁各CEO積極了解區塊鏈，并立即動員全體高管和員工，學習如何擁抱這場革命。[2018/1/9]

Z(n+1)=1

2.乘法循環群剛好可以滿足這個條件，如果設計一個階為n的一個乘法循環群H，根據群的性質可以知道Z(g)=Z(g^(n+1))。因此，在設計Z時，會保證Z(g)=1；上圖中的自變量的取值也將從{1...n}變成{g...g^n}。所以在上圖中驗證的部分，a其實已經換成了群H里的所有元素。

3.根據論文中的協議，多項式Z是會發給可信第三方I驗證方V會從I處獲取到多項式Z在所有a處的取值，然后依次校驗。

下面具體看一下論文中的定義：

從定義中可以看出：多項式f,g在范圍內具有相同的值的集合；下面看一下論文中具體的協議部分，結合上述解釋的3點：

說明：圖4中的f,g對應圖3中的f。即f,g是同一個多項式。其實只要是相同的值的集合，也可以不用于是同一個多項式。圖3是一個特例而已。

跨多項式的校驗

其實就是證明對于某個多項式f，g，存在兩個點x,y，滿足f(x)=g(y)。與存在兩處不同：

多個多項式；不強制x,y的關系，即也可以等，也可以不等；有了(1)小節的基礎，這次我們先看一下相關的定義：

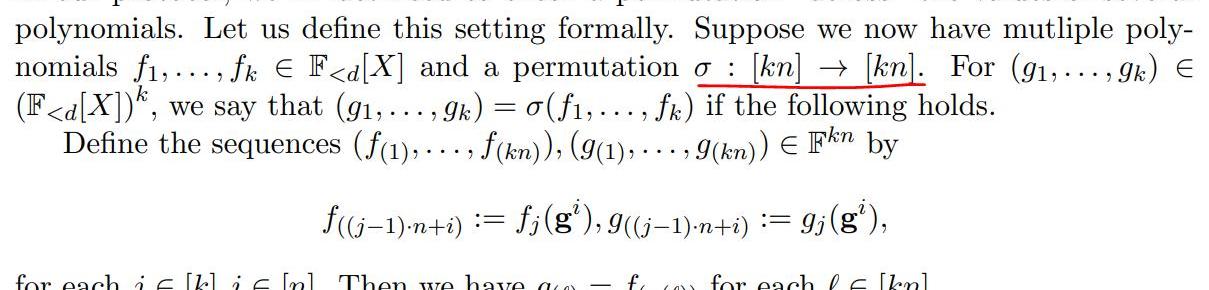
從定義可以看到，這次是兩個多項式集合見的置換校驗算法。從標注的部分可以看出：

兩個多項式集合仍然具有相同的值的結合；為了區分集合里的多項式，自變量的索引得區分開來；因此，可以想象的到，如果存在兩個多項式f,g，想要證明f(x)=g(y)，那么根據以上描述可以判斷{f1,f2}={f,g}={g1,g2}。也保證了上述第1點的成立。

下面我們看一下具體的原理：

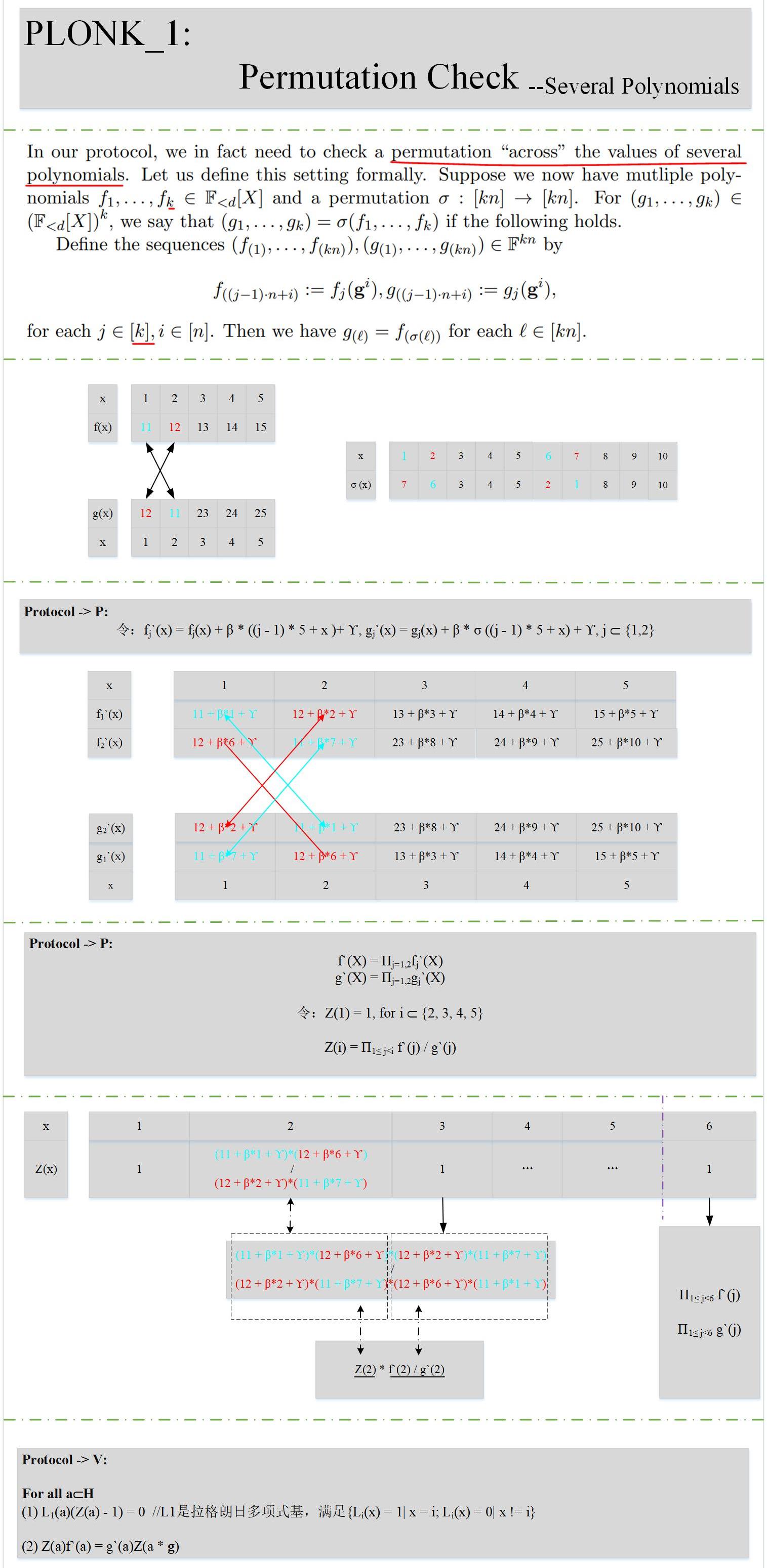
和(1)小節相比，證明方P增加了些工作量，驗證方V工作量不變。結合上述描述，也能很容易的理解其數學原理。

說明：至此，其實我們已經慢慢的接觸到PLONK算法的核心了，前面我們講到，電路的滿足性問題除了門的約束關系還有門之間的約束關系。

比如一個輸入x，它既是一個乘法門的左輸入，又是另外一個乘法門的右輸入，這就需要去證明L(m)=R(n)，這就是跨多項式的置換校驗。

下面再給出論文里的協議內容：

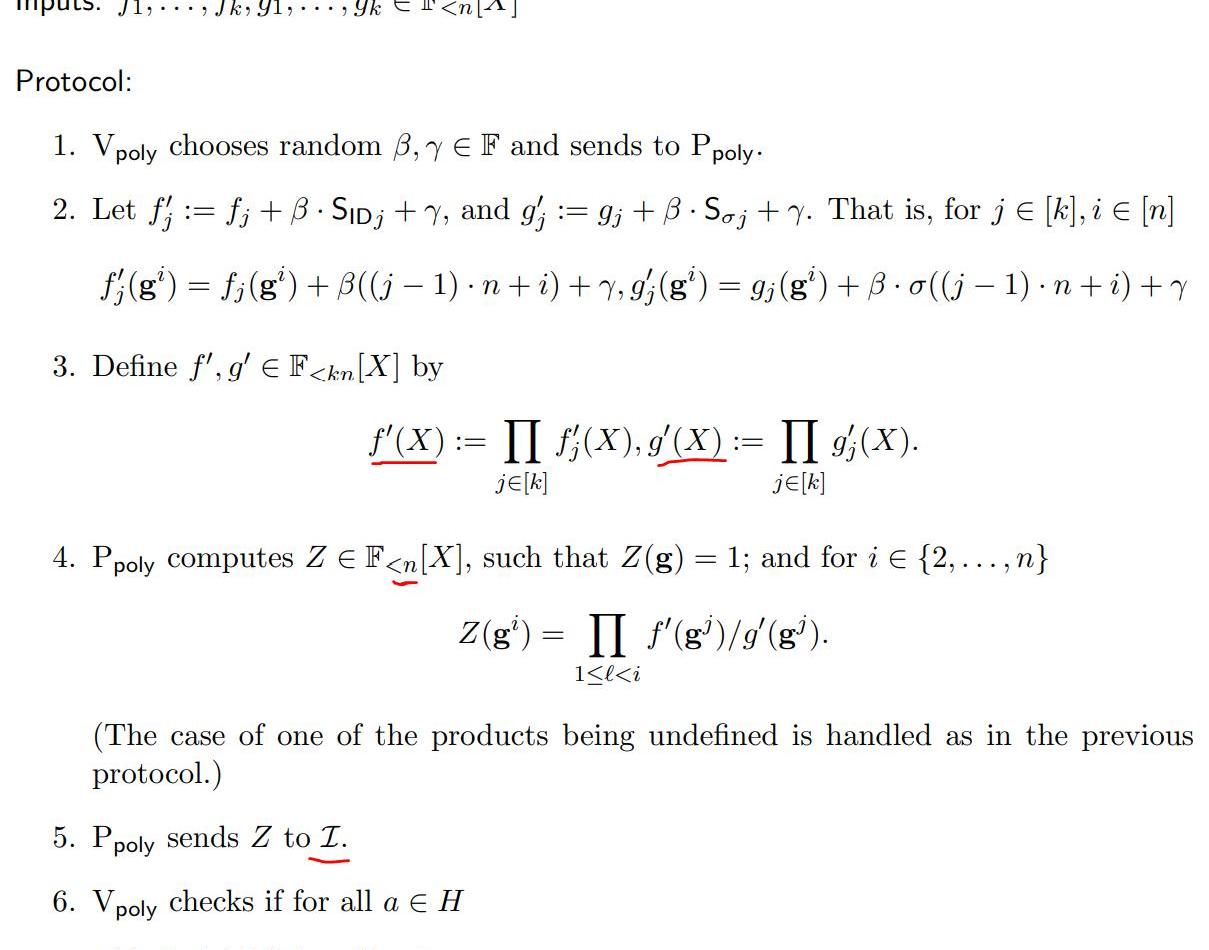
至此，本篇文章已經描述了，在PLONK算法里，電路的設計以及復制約束的成立驗證兩大部分，接下來，將會另起一片文章，去分享門約束的成立和整個協議的具體步驟。

以上都是作者小白的個人理解，還希望各位讀者多多指教，謝謝。

Tags：PLOLON區塊鏈CRSWhale ExploderCyclone區塊鏈的幾個大騙局有哪些crs幣是什么意思

FIL幣