科普 | 天冷了，干了這碗“零知識證明”雞湯_ROT

前言：從一鍋雞湯說起

當讀者剛開始接觸零知識證明的概念時，面臨第一關就是如何搞懂突如其來的大量名詞，比如離散對數問題、雙線性對還有Groth16、PLONK、RedShift等。不妨我們借用“烹飪”這個生活場景來類比其中的層次關系。

如果把“密碼學”比做“烹飪”，那么上個系列中對雙線性對的學習就類似于學習燉湯前先簡單了解的高壓鍋的工作原理，而zkSNARK則相當于在說明如何用高壓鍋燉出美味雞湯。

由此可見，雙線性對是類似基礎工具的角色：就像高壓鍋既可以燉雞湯也可以燉排骨湯，雙線性對既可以用于零知識證明也可以用于構造簽名等密碼學算法。而Groth16、PLONK、RedShift等，它們同屬于zkSNARK，屬于同一層次，如果沿用上述類比，那大概就是對應用高壓鍋做湯的風味選擇了。Groth16算法是JensGroth提出的一種zkSNARK算法，相關論文不僅對已有算法進行改進，而且討論了基于配對的非交互式零知識論證的證明大小問題。Groth16因其精簡的證明大小和高效的驗證效率，在ZCash等項目中多有應用，是最經典的零知識證明算法之一。

穩定幣crvUSD科普創新清算機制LLAMMA，可在抵押品價格下跌時逐步替換為穩定幣:1月17日消息，Curve官方科普其穩定幣crvUSD創新的清算機制LLAMMA，解釋了LLAMMA通過AMM的特性進行針對債務人更友善的清算方式，讓抵押品在價格下跌時逐漸轉移成穩定幣，讓原本要清償的債務有一定程度的穩定幣可以償還，同時在價格回穩時再逐漸把穩定幣換回抵押品，而不是直接的觸發清算導致債務人的虧損。

此前報道，2022年11月23日，去中心化交易平臺CurveFinance開發者發布Curve即將推出的去中心化Stablecoin“crvUSD”的官方代碼和白皮書。[2023/1/17 11:17:13]

上一個系列中我們完整介紹了零知識證明中用到的橢圓曲線和雙線性配對相關的基礎知識。本系列通過動手算的方式，以Groth16算法為例，循序漸進地介紹zkSNARK的基本原理。

歐科云鏈集團正式啟動區塊鏈科普行動“星途計劃”:歐科云鏈集團于4月26日，正式宣布啟動了區塊鏈科普行動——“星途計劃”，行動包括將在全國范圍展開系列沙龍，加大力度推進區塊鏈科普進機關、進國企、進校園等，聯合政府部門、行業協會等共同構建起更加完善和有效的區塊鏈科普教育生態，與此同時，直擊區塊鏈科普現存痛點，推出簡單易懂的“秒懂區塊鏈”公益短視頻課。

該計劃旨在全維度推動社會建立對產業更清晰的認知，與“鯤鵬計劃”一道助力數字經濟及區塊鏈產業本身健康發展夯實“人才”和“產業認知”兩大基礎。[2021/4/26 20:59:37]

本篇是“動手算Groth16”的上篇，主要介紹如何從程序轉化為電路和描述算數電路的一種約束系統R1CS。下篇會介紹如何從R1CS轉化為多項式相關的約束問題，并且詳細給出完整的Groth16從頭到尾的手算步驟。

程序與電路

聲音 | 浪潮集團云南分公司總經理：云南區塊鏈產業發展需從“科普”到“專精”不斷深化:據昆明日報消息，浪潮集團云南分公司總經理鄭昕表示，云南區塊鏈產業發展需從“科普”到“專精”不斷深化。下一步，浪潮將繼續加大云南農業產業高質量發展體系建設力度，重點以普洱茶等云南優勢產業為切入點，打造云南“綠色、有機農產品高地”的品牌形象，并在此基礎上，開展基于區塊鏈的供應鏈金融服務，解決中小企業貸款難、貸款貴問題。[2019/11/11]

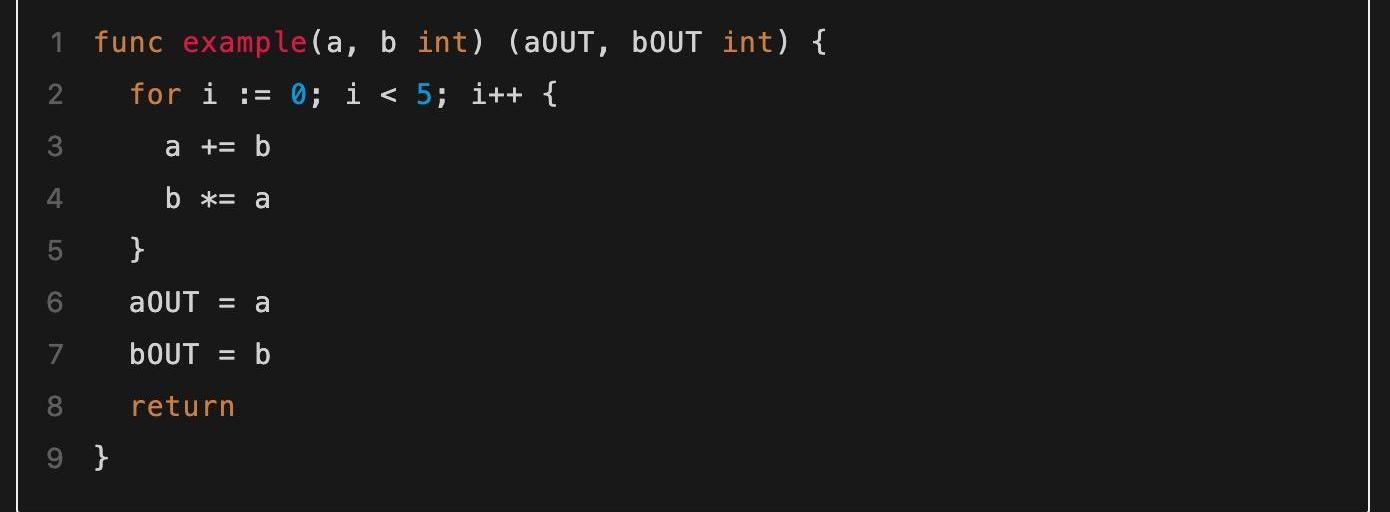
初始接觸通用零知識證明算法時，讀者可能最容易感到疑惑的地方就是各種資料中頻繁提到的“電路”一詞。這里的“電路”是指什么？它又如何等價地對同一個問題進行描述呢？回答這些問題最簡單的方式就是使用具體的一個算法例子進行說明。比如我們有下面一段程序代碼，如何將其轉化為等價的電路呢？

聲音 | ETC Labs主管：科普教育是未來幾年公鏈面臨的巨大挑戰:ETCLabs主管Darin Kotalik認為，科普教育是未來幾年公鏈面臨的巨大挑戰，人們必須要對區塊鏈有基本的認識，分清楚公鏈和私鏈的區別。[2019/8/25]

▲需要被轉化為電路的代碼

這里需要注意到程序中值被存儲在變量中，而電路中的值是用電路門之間的連線表示的。這其中有個關鍵的不同是：變量的值是會隨著時間變化的，而電路中連線的值是固定不能改變的。因此首先我們通過引入一些中間量的方式表示隨循環而不斷變化的各階段的變量值，中間量命名為tmp1,tmp2...這樣的形式：

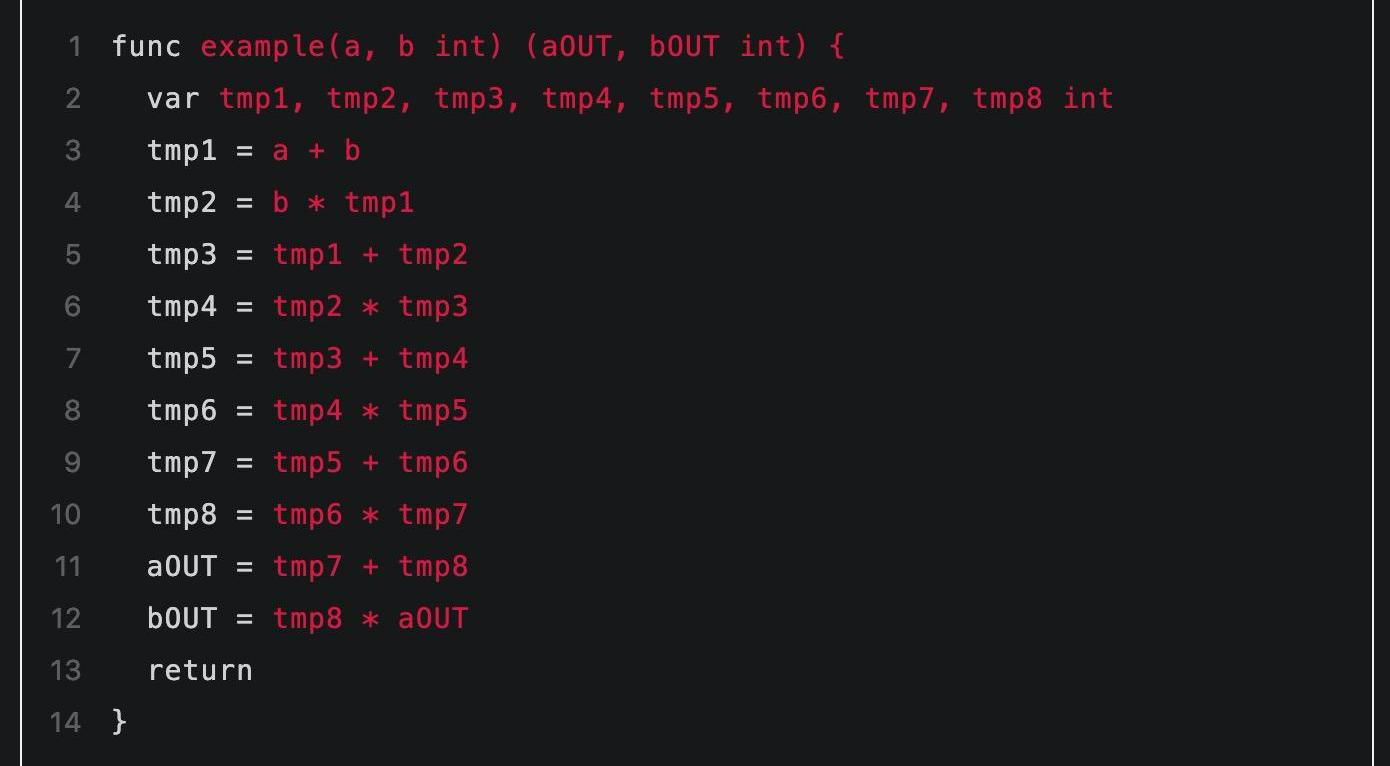
▲引入輔助的中間量

最后我們可以轉化為只有加法門和乘法門的算數電路：

聲音 | 火星人朋友圈科普RAM:火星人在朋友圈發文稱，“什么是RAM？簡單來說就是EOS這個國家的土地，所有的經濟行為都離不開土地。只要EOS的BP們能投票形成一個穩定的供給預期，并且不改變目前的Bancor算法，那么RAM后續的價格有可能會像北上廣深的房價走勢。房價下跌不行，房價過快上漲也不行，EOS的生態越來越像某國了，真有意思。”[2018/7/6]

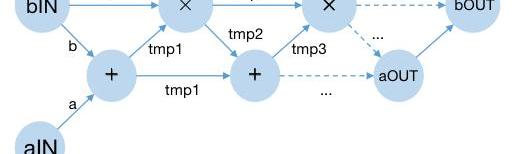
▲電路示意圖

這里除去輸入和輸出外，其他的圓圈代表了電路中的門：可以是乘法門或者加法門。而門和門之間的連線對應了程序中的中間變量在某個時刻的值。

如果站在更高的角度思考，其實可以發現有很多結構都能實現“運算”功能，比如說神經元組成的人腦，比如馮·諾伊曼結構的計算機，甚至更早的機械計算器和當今的人工神經網絡。算數電路也是這樣的一種能夠完成一定運算的結構，而且基于這種結構我們能夠完成對計算輸入和過程的“零知識證明”。因此通用零知識證明算法普遍引入了“電路”這個運算結構并且會研究，如何更好的將高級語言描述的問題轉化為等價的算法電路。

上面例子中約束較多，會給后續的“動手算”產生較多的計算量壓力，因此在下文中我們以一個新的例子重新展示這個轉化的過程。本系列后續文章都會以這個新的例子為主線進行敘述，從而真實展示證明和驗證的具體計算過程。新例子的程序代碼如下：

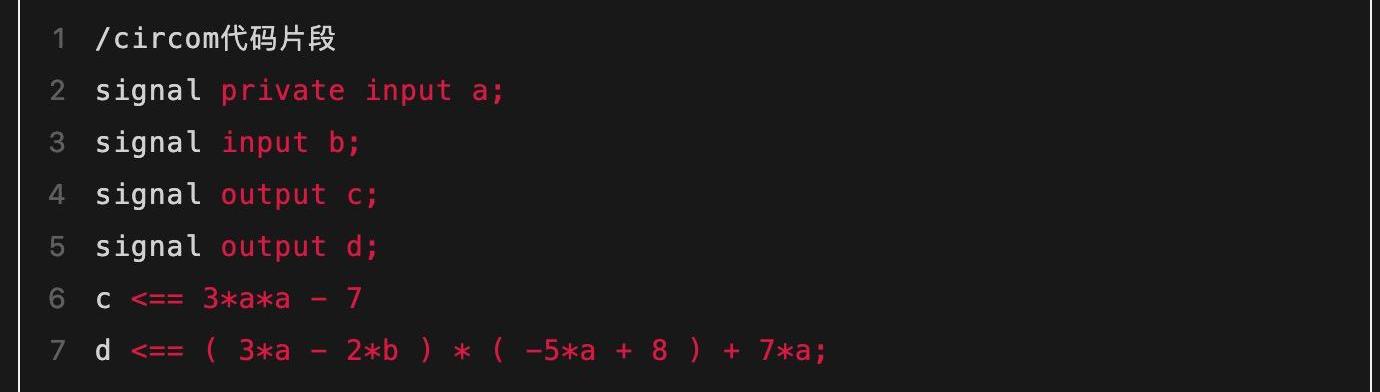
這里涉及到4個連線以及兩個等式關系。這兩個等式關系用更規范的方式重寫一下可以幫助讀者看地更清晰：

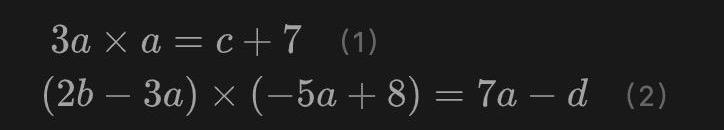
觀察這兩個式子的特點，可以發現兩個等式關系其實都可以寫作A×B=C的形式，其中A、B和C都是變量的“加權組合”。這并非巧合，而是我們有意為之。通過這種形式我們避免了對加法門的約束產生額外開銷，而是在對乘法門進行約束的同時零開銷的對加法關系進行約束，這是groth16的特點之一。在Groth16算法中，加法門和乘法門的地位并不是等價的，我們更關心乘法門。

下面對a,b,c,d四個變量賦予編號，以便下一步的處理,按照groth16的習慣我們將輸出排列在輸入之前：

可以看到除了連線a、b、c和d，還有一個特殊的連線“1”，“1”其實可以看作是一個特殊的公共輸入，他的存在讓我們在算法中能更容易地處理常量。“1”的值總是1。

從電路到R1CS

本部分之前先回顧一下向量的內積概念，向量的內積是從兩個同維向量得到一個標量的運算，其幾何意義對應了“投影”這個概念。比方說兩個二維向量的乘法：

·=2×4+3×1=11

回過頭看剛才的結果，因為A×B=C這個形式的存在，我們其實能夠進一步的對這些等式關系進行抽象。抽象的目的是為了方便編程處理和下一步的討論。以式子(2)為例，我們其實可以認為他是如下的形式：

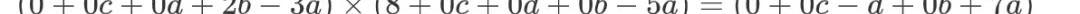
根據上面介紹的向量內積，可以發現這里的A，B，C其實都是向量內積的形式:

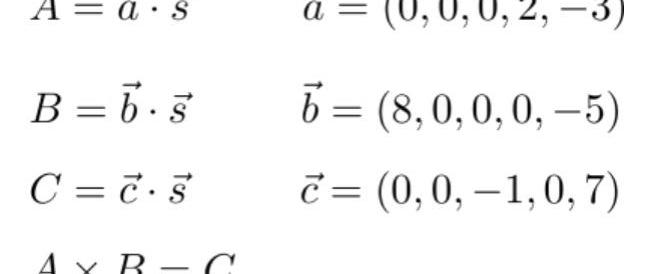
這里的s其實就是全部的連線的值，如果證明者P是真的計算過這個電路的，則P能夠獲知s的值，否則P無法得知s的值。我們將這個s稱為witness。因此通過上面的向量a,b,c我們就能夠對s進行一定的約束，即s應該滿足：

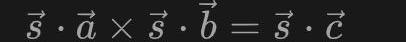
這就構成了一個一階約束,這樣的一個約束對應了電路中的一個乘法門。如果我們將所有的約束聯立起來，就得到一個一階約束系統。通過R1CS我們可以更方便的形式化描述一個零知識證明問題，從而為我們后續解決該問題提供了條件。

下篇我們會介紹如何將R1CS描述轉換為多項式描述，并且通過完整的計算過程展示groth16算法的相關內容，敬請關注。

Tags：ROTGRO區塊鏈穩定幣Vesta ProtocolSB Groupaia幣區塊鏈穩定幣有哪幾種形態

比特幣價格