零知識證明： Plookup算法介紹_LOOK

最近有空看了看Plookup的論文。針對對電路描述不友好的操作（比如bit操作），Plookup給出了新的思路和證明方式。給定某個操作的真值表示（lookup table），證明某個操作的輸入/輸出是在真值表中。這種方式，相對之前的bit計算約束方式，降低約束的個數，提高了電路效率。

Plookup的論文下載地址如下：

https://eprint.iacr.org/2020/315.pdf

基本思想

Plookup嘗試解決的問題是，給定兩個集合，證明某個集合的元素在另外一個集合中。給定兩個集合t和f，s是f排序后的結果。如果t中的元素最少在f中出現過一次。判別f中的元素是否包括在t中，只需要比較元素差的集合：

零知識身份預言機提供商zkMe完成200萬美元Pre-Seed輪融資，Circle Venture等參投:5月30日消息，零知識身份預言機 zkMe 完成 200 萬美元 Pre-Seed 輪融資，Circle Venture、Spartan Group、CMS Holdings、Fenbushi Capital、NGC Ventures、Arkstream Capital 等參投，計劃利用新資金加速開發，在一個月內完成主網測試并上線客戶注冊功能。

ZkMe 允許用戶加密他們的數據，并使用 ZKP 在他們自己的設備上證明聲明，以有效地驗證用戶資格，同時保護他們的隱私安全。[2023/5/30 9:49:53]

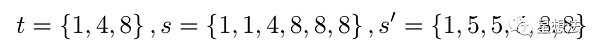
以太坊基金會更新支持的研發項目，涉及零知識證明的項目數量最多:4月27日消息，以太坊基金會公開了正在支持的研發團隊的項目和領域，其中涉及“應用零知識證明”的團隊和技術最多，近14個項目。

除了零知識證明之外，以太坊基金會還支持了關于ETH2研究、以太坊基金會官網、Ewasm、形式化驗證、Geth客戶端、Javascript團隊、Remix、無狀態客戶端、Solidity等領域。[2021/4/27 21:03:39]

舉個例子，t是{1，4，8}的集合，元素的差異集合為{3, 4}，分別是4-1，8-4。如果s只有t中的元素組成，并且每個元素最少出現一次，例如{1，1，4，8，8，8}，元素的差異集合也為{3，4}。如果s中的元素并不完全是t中的元素，那即使在元素差異集合一樣的情況下，也不能說明s中元素在t的集合中。例如s為{1，5，5，5，8，8}，元素的差異集合也為{3，4}，分別是8-5，5-1。

動態 | 以色列理工學院教授違反知識產權規定建立零知識證明技術公司:據Bitcoin.com報道，以色列理工學院教授Eli Ben-Sasson因違反了該學校知識產權規定而被起訴。據報道，Ben-Sasson利用在為該機構工作時開發的知識產權建立了一家零知識證明技術公司。Ben-Sasson是區塊鏈技術初創公司Starkware的聯合創始人兼首席科學家，以色列理工學院在法庭提出要求Ben-Sasson轉讓其在該公司的50%股份。[2019/4/23]

論文提出，可以引入一個隨機因子，將前后兩個元素相加的方法，確定兩個集合的依賴關系。

定義多項式

在基本思想的基礎上，論文在第三章定義了兩個多項式F和G：

如果F和G相互對等，有且如下的條件成立：

f集合屬于t

s是(f，t)的并集，并且按照t中的元素排序

如果條件成立，可以推導出兩個多項式相等。F多項式可以看成是兩部分組成，分別是兩個連乘。后面的連乘可以看成是t中的元素連乘。前面的連乘，可以看成是f中元素的連乘。因為f中的元素屬于t，則f中的元素的連乘，可以想象成多個相同元素的連乘。反之，因為beta和gamma的隨機因子，也能從F和G對等條件推出滿足的兩個條件。具體的證明過程，可以查看論文的第三章。

在定義多項式的基礎上，問題可以轉化成兩個多項式相等。

Plookup協議

已知f和t，可以排序得到s。因為s由f和t合并而成，s可以由兩個函數h1和h2表示。關鍵在于第4步，定義了Z函數：

Z(g) = 1 - 初始為1

Z(x) 是兩種多項式表示的商

Z(g^(n+1)) = 1 - n+1元素的連乘，兩種多項式表達式相等

驗證者，除了查看Z函數外，額外還要查看h1/h2連續性。

論文進一步將協議推廣到更通用的情況，并給出了t中元素是連續情況下的優化協議。感興趣的小伙伴可以自行查看。

Plookup提出了一種明確輸入/輸出的情況下，如何證明某個函數的運算正確的協議。輸入輸出定義成lookup表，計算的輸入/結果只要在該lookup表中即表示運算正確。和Plonk采用同樣的思路，Plookup定義了問題的多項式表示，證明了Z函數的遞歸表示和邊界。

Tags：LOOKOKUPLOSONlooks幣未來一個多少錢Kazoku INUPloutozSonar Token

火必交易所